Santa Claus’ optimized delivery process

There are many blog posts out there about the general principle and how to do it with reindeer and a sleigh. For example, ‘Santa Routing and Heuristics in Operations Research‘, ‘How I saved Christmas with the Travelling Salesman Problem‘ and ‘The flight route of Santa Claus‘.

However, what I didn’t find is how long Santa’s route would need to be in order to visit all households around the world.

While the exact number of locations is hard to pinpoint, that’s no reason to leave an interesting problem unsolved. We can always go for an approximate solution and change the inputs to increase understanding. 

The University of Waterloo has a great encyclopaedia page about TSP problems. Just look at these pictures!

Here, you will find the shortest route for visiting all the 49 687 pubs in the UK. For cyclists, a tour to visit all 57 912 monuments in the Netherlands. And for Elon Musk, a route to visit 1.33⠐ 10⁹ stars when he gets bored with Mars. But more importantly, there is also the shortest known route for visiting all the 1 904 711 cities in the world. 

Finding the shortest route between a number of locations is no easy feat, because of the combinatorial nature of the problem. The number of possible routes to choose from is (n-1)!, which can be approximated using Stirling’s formula to:

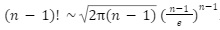
By putting in the number of cities we get:

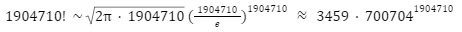
This is probably larger than any number you’ve ever heard. Transforming to more familiar base-10 notation we get this:

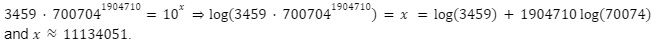
So, in conclusion, there are 1904710! > 10^{10 000 000} options to choose between. Looking at that number it is pretty impressive that the current shortest solution to the problem is only 0.0471% longer than the optimal route.

Visit our ‘Technology’ category page to read more blog articles.

Santa will have to fly around 7 515 756 km to visit all the cities in the world

The solution is that Santa would have to fly around 7 515 756 km in order to visit all the cities in the world. That is a baffling 188 times around the globe or almost 10 times to the moon and back. 

Even putting that number into context, it feels somewhat detached from reality. Let’s use something more ordinary like Finland: Finland is after all a pretty average country (65th in terms of size and 115th in population out of 190-ish), plus it is Santa’s home.

Using the same data source as previously, we find that there exists an optimal shortest path for visiting the 10 639 largest settlements in the country! This optimal route is merely 54 020 km long.

I must however admit I would not be too happy if Santa just left my presents in the market square. Consumers are fairly demanding, and nothing short of home delivery is acceptable with regard to their Christmas presents. 

How much extra distance does the last mile delivery add to this optimal route?

I am not aware of a dataset that includes the addresses of all Finnish inhabited households. Also if there was one, I’d probably violate GDPR by using it, so let’s go with an approximate solution instead.

Suppose we’re operating on a flat surface and consider a square the size of 1km². We assume further that there are n visiting locations randomly distributed on the surface and denote the shortest path visiting all of these by L_n.

Interestingly enough, it’s not yet known what the expected shortest path length E(L_n) is! 

There are however bounds for it. According to Wikipedia, it’s almost surely in the following interval:

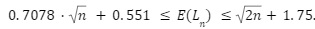
So, for 100 randomly scattered households in a given square kilometre, Santa could expect to travel at least 7.62 km and at most 15.89 km.

That’s quite a wide interval and looking at some computational studies, we notice that the upper bound is definitely too conservative. There is also Steinerberger (2014) showing a considerably narrower theoretical interval:

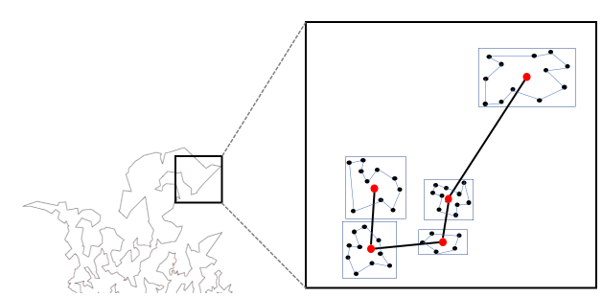
There are approximately 100 000 populated square kilometres in Finland, 100 338 to be exact. The average household size is 2.02, so we can divide each square’s population by that number to get the number of visiting locations.

Considering that some of the inhabited squares are actually very sparsely populated, the most advisable course of action is to use the computational estimates for squares with sparse populations and the theoretical bounds for the densely populated areas.

Out of these squares, 96 125 have less than 100 households. Let’s use computational estimates for these and theoretical bounds for the rest. For squares with 1 household, we assume within-square travel to be zero. This gives us a total route length of 210 000 – 232 000 km from within-square travel. 

There is one slight issue though – 100 338 is somewhat higher than the number of settlements in our optimal route (10 639), so we have to do some hand-waving applied mathematics. 

We could “squeeze” population into the 10 639 most populated squares in the data set. This would result in an underestimate of the within-square travel, because higher population density leads to more efficient last-mile delivery. 

We can also just add the numbers together and ignore any travel between populated squares, which isn’t covered by the original shortest route. This leads to a slight underestimate of the total route length. 

On the other hand, assuming a random distribution on the populated squares is not completely realistic—settlements are usually clustered in some way—which means that we have a slight overestimate on the within-square-travel. 

To summarise, the approximations partly cancel each other out and I am just going to add the numbers together.

In conclusion, Santa has around 275 000 km of domestic travel to expect on Christmas Eve. Traditions in families differ, but most presents are given out between 15 and 19 o’clock.

That gives an average speed of 68 750 km/h ~ 19 km/s. That is not completely out of this world: Spacecraft sometimes travel faster than that. At least if Santa seems to be in a hurry, now you know why!

As a final note, one word of caution. Despite the chilly weather, offering Santa a whiskey shot for warming up is definitely not recommended. If just one in ten households offers him 2cl of whiskey, already by the midpoint of his route poor Santa’s blood alcohol content is asymptotically approaching 1000 ‰.